Factorial Design SpringerLink

Table Of Content

• What is a full factorial and fractional factorial design?
• Non-Manipulated Independent Variables
• Book traversal links for Lesson 5: Introduction to Factorial Designs
• Factorial Design
• Selecting Factors: Factor and Intervention Component Compatibility
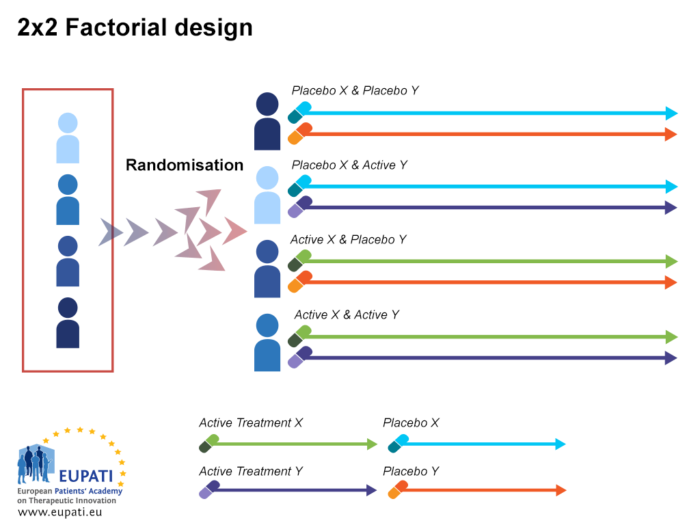
• 3.1. 2x2 Factorial designs¶
• IV. Chapter 4: Psychological Measurement
• Setting Up a Factorial Experiment

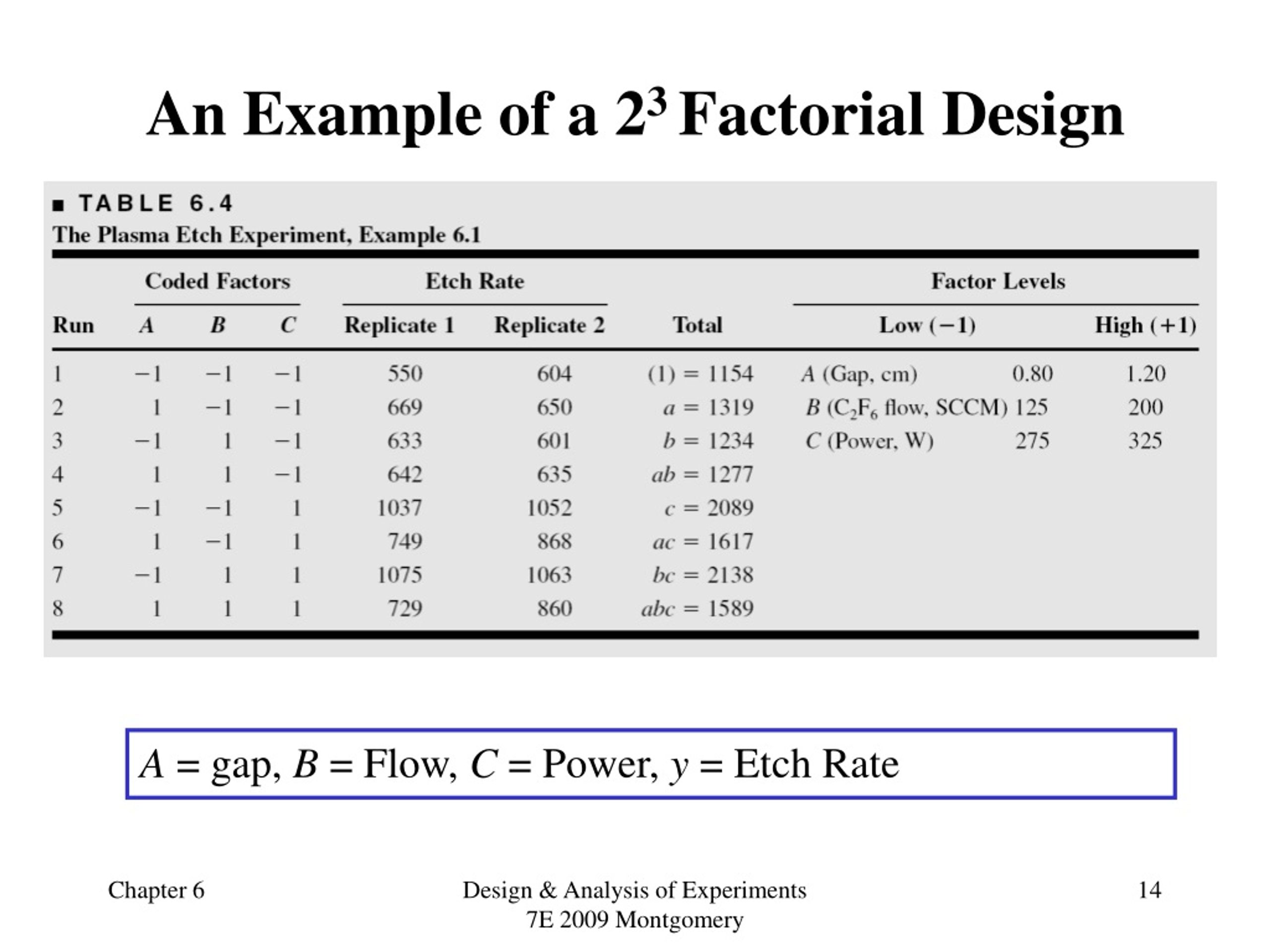
Sometimes, those groups were unrelated (independent t-test) and sometimes they were related (dependent t-test). Sometimes those IV levels were unrelated (Between Groups ANOVA) and sometimes they were related (Repeated Measures ANOVA, sometimes called Within-Groups ANOVA). Suppose that you are looking to study the effects of hours slept (A), hours spent with significant other (B), and hours spent studying (C) on a students exam scores. You are given the following table that relates the combination of these factors and the students scores over the course of a semester.

What is a full factorial and fractional factorial design?

In sum, in a factorial experiment, the effects, relative effects, and statistical significance of ICs will likely change depending upon the number and types of components that co-occur in the experimental design. This arises, in part, from the fact that the effects of any given factor are defined by its average over the levels of the other factors in the experiment. It is important, therefore, for researchers to interpret the effects of a factorial experiment with regard to the context of the other experimental factors, their levels and effects.

Non-Manipulated Independent Variables

In sum, investigators should be cognizant of the possible effects of such intervention adjustment and consider options for addressing them (e.g., by making only essential adjustments to a component, nesting an adjusted factor in the design). These ideas can be confusing if you think that the word “independent” refers to the relationship between independent variables. However, the term “independent variable” refers to the relationship between the manipulated variable and the measured variable.

Book traversal links for Lesson 5: Introduction to Factorial Designs

When you conduct a 2x2 design, the task for analysis is to determine which of the 8 possibilites occured, and then explain the patterns for each of the effects that occurred. This kind of design has a special property that makes it a factorial design. That is, the levels of each independent variable are each manipulated across the levels of the other indpendent variable. In other words, we manipulate whether switch #1 is up or down when switch #2 is up, and when switch numebr #2 is down.

Since the high and low levels for each factor may not be known when the design is first created, it is convenient to be able to define them later. Factors A - D can be renamed to represent the actual factors of the system. Additionally, a low and high value are initially listed as -1 and 1, where -1 is the low and 1 is the high value. The low and high levels for each factor can be changed to their actual values in this menu.

Factorial design formulation optimization and in vitro characterization of curcumin-loaded PLGA nanoparticles for colon ... - ScienceDirect.com

Factorial design formulation optimization and in vitro characterization of curcumin-loaded PLGA nanoparticles for colon ....

Posted: Sat, 23 Dec 2017 17:58:22 GMT [source]

Typically, if the same experimentation will occur for 3 lab periods, 2 replicates will be added. Replicates are repeats of each trial that help determine the reproducibility of the design, thus increasing the number of trials and accuracy of the DOE. To add replicates, click the "Replicate design" radio button in the "Modify Design" menu. Once the design has been chosen, the "Factors...", "Options..." and "Results..." buttons become active in the "Create Factorial Designs" option menu. After the number of factors is chosen, click on the "Designs..." option to see the following menu.

Although she was primarily interested in how the odors affected people’s creativity, she was also curious about how they affected people’s moods and perceived health—and it was a simple enough matter to measure these dependent variables too. Although she found that creativity was unaffected by the ambient odor, she found that people’s moods were lower in the dimethyl sulfide condition, and that their perceived health was greater in the lemon condition. The research designs we have considered so far have been simple—focusing on a question about one variable or about a statistical relationship between two variables. But in many ways, the complex design of this experiment undertaken by Schnall and her colleagues is more typical of research in psychology. Fortunately, we have already covered the basic elements of such designs in previous chapters.

IV. Chapter 4: Psychological Measurement

Including numerous factors might also increase the occurrence of interactions, which might affect the magnitude of a main effect (despite the lack of correlation between main and interaction effects with effect coding). In addition to looking at the employment sector, the researchers also look at gender. In this example, the employment sector and gender of the graduates are the independent variables, and the starting salaries are the dependent variables. So, for example, a 4×3 factorial design would involve two independent variables with four levels for one IV and three levels for the other IV.

Suppose you have two variables \(A\) and \(B\) and each have two levels a1, a2 and b1, b2. You would measure combination effects of \(A\) and \(B\) (a1b1, a1b2, a2b1, a2b2). Since we have two factors, each of which has two levels, we say that we have a 2 x 2 or a 22 factorial design. Typically, when performing factorial design, there will be two levels, and n different factors. Because factorial design can lead to a large number of trials, which can become expensive and time-consuming, factorial design is best used for a small number of variables with few states (1 to 3). Factorial design works well when interactions between variables are strong and important and where every variable contributes significantly.

An example is a study by Halle Brown and colleagues in which participants were exposed to several words that they were later asked to recall (Brown, Kosslyn, Delamater, Fama, & Barsky, 1999)[1]. For example, a researcher might choose to treat cell phone use as a within-subjects factor by testing the same participants both while using a cell phone and while not using a cell phone (while counterbalancing the order of these two conditions). But he or she might choose to treat time of day as a between-subjects factor by testing each participant either during the day or during the night (perhaps because this only requires them to come in for testing once). In sum, unless the investigator has access to clearly relevant data (preferably from factorial experiments) s/he should have strong concerns about how the elements in a treatment (the ICs) might interact.

Characterization of industrial ceramic glazes containing chromite processing waste: Experimental factorial design ... - ScienceDirect.com

Characterization of industrial ceramic glazes containing chromite processing waste: Experimental factorial design ....

Posted: Fri, 15 Apr 2022 07:00:00 GMT [source]

By the traditional experimentation, each experiment would have to be isolated separately to fully find the effect on B. Note that only four experiments were required in factorial designs to solve for the eight values in A and B. A main effects situation is when there exists a consistent trend among the different levels of a factor. From the example above, suppose you find that as dosage increases, the percentage of people who suffer from seizures increases as well.

The experiment can be replicated, or the sparsity-of-effects principle can often be exploited. Replication is more common for small experiments and is a very reliable way of assessing experimental error. When the number of factors is large (typically more than about 5 factors, but this does vary by application), replication of the design can become operationally difficult. In these cases, it is common to only run a single replicate of the design, and to assume that factor interactions of more than a certain order (say, between three or more factors) are negligible.

Recall that Schnall and her colleagues were interested in the harshness of people’s moral judgments. To measure this construct, they presented their participants with seven different scenarios describing morally questionable behaviors and asked them to rate the moral acceptability of each one. Although the researchers could have treated each of the seven ratings as a separate dependent variable, these researchers combined them into a single dependent variable by computing their mean. When an experiment includes multiple dependent variables, there is again a possibility of carryover effects. For example, it is possible that measuring participants’ moods before measuring their perceived health could affect their perceived health or that measuring their perceived health before their moods could affect their moods. So the order in which multiple dependent variables are measured becomes an issue.

Line graphs are also appropriate when representing measurements made over a time interval (also referred to as time series information) on the x-axis. It is tempting to take advantage of the efficiency of the factorial experiment and use it to evaluate many components since power is unrelated to the number of factors, and therefore, a single experiment can be used to screen many components. However, the number of factors used and the types and number of levels per factor can certainly affect staff burden. A 5-factor design with 2-levels/factor yields some 32 unique combinations of components (Table 1), and requires that at least five different active or “on” ICs be delivered. Moreover, if instead of “off” or no-treatment conditions, less intensive levels of components are used, then even more ICs must be delivered (albeit some of reduced intensity). To illustrate a 3 x 3 design has two independent variables, each with three levels, while a 2 x 2 x 2 design has three independent variables, each with two levels.

This is because research shows that the effectiveness of a IC can be substantially modulated by the other ICs with which it is used (Cook et al., 2016; Fraser et al., 2014; Schlam et al., 2016); i.e., they may interact. If one of the independent variables had a third level (e.g., using a handheld cell phone, using a hands-free cell phone, and not using a cell phone), then it would be a 3 × 2 factorial design, and there would be six distinct conditions. Notice that the number of possible conditions is the product of the numbers of levels. A 2 × 2 factorial design has four conditions, a 3 × 2 factorial design has six conditions, a 4 × 5 factorial design would have 20 conditions, and so on. Also notice that each number in the notation represents one factor, one independent variable. So by looking at how many numbers are in the notation, you can determine how many independent variables there are in the experiment.